一、相關(guān)性和回歸分析在六西格瑪突破模式各階段的作用
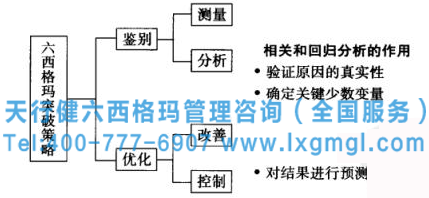
從圖1可以看出,相關(guān)回歸分析可以驗證輸入因素與輸出結(jié)果之間關(guān)系的真實性,即原因的真實性,確定六西格瑪突破戰(zhàn)略分析階段的“關(guān)鍵少數(shù)因素”。這是六西格瑪分析階段的主要任務(wù)。在控制階段,相關(guān)和回歸分析可以根據(jù)輸入的變化預(yù)測輸出結(jié)果,以確定是否應(yīng)該調(diào)整輸入。

圖1 相關(guān)和回歸分析在六西格瑪突破模式各階段的作用
二.相關(guān)分析概述
1.變量之間的相關(guān)性
示例:某工藝工程師想研究松香比重對焊點拉拔力的影響,測得一組數(shù)據(jù)如下圖2所示:
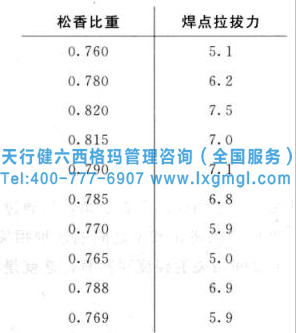
圖2 松香比重對焊點拉拔力的影響數(shù)據(jù)測量
如果仔細觀察這組數(shù)據(jù),我們會發(fā)現(xiàn)一個規(guī)律,當(dāng)松香比重增大時,焊點的拉拔力也會相應(yīng)增大,這說明焊點的拉拔力與松香比重之間是有關(guān)系的,我們稱之為松香比重與焊點拉拔力的相關(guān)性。
2.散點圖
散點圖就是用圖形表示一對變量,兩個變量分別對應(yīng)圖上的X和Y坐標軸,這樣每對對應(yīng)的X和Y數(shù)據(jù)就可以用散點圖上的一個點來表示。通過觀察散點圖的形狀,可以直觀地了解變量X和y之間的關(guān)系。
松香比重與焊點拉拔力之間的關(guān)系可用散點圖表示如下:
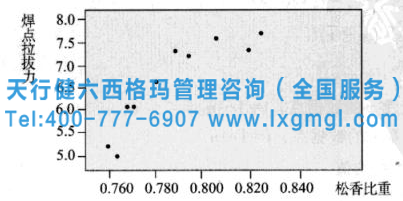
圖3 散布圖-松香比重和焊點拉拔力的關(guān)系
從圖3的散點圖中,我們可以看到一個規(guī)律:數(shù)據(jù)分布是一條細細的帶狀(在一個帶狀范圍內(nèi)),從圖表的左下角延伸到右上角。但是從上圖我們能知道的信息很粗略。怎樣才能量化X和Y的相關(guān)性,有沒有一個參數(shù)來衡量X和Y的相關(guān)性?是的,這就是我們將要討論的相關(guān)系數(shù)。
3.相關(guān)系數(shù)
相關(guān)系數(shù)是用來描述變量,x和y之間線性相關(guān)程度的參數(shù),用r來表示,它具有以下特性。
①r的值介于(-1, 1)之間。
②r的絕對值越接近1表示x和Y之間的線性關(guān)系越密切。
③r>O,x與y呈正相關(guān),r<0,x與Y呈負相關(guān),r=O,x與y之間無線性相關(guān)關(guān)系。